10 Types of Spatial Awareness Tests in 2024
Updated November 10, 2023
- What Are Spatial Ability Tests?
- Why Do Employers Use Spatial Reasoning Tests?
- Why Do Employers Use Spatial Ability Tests?
- What to Expect on a Spatial Ability Test
- Examples of Spatial Reasoning Questions: 10 Types
empty
empty
empty
empty
empty
empty
empty
empty
empty
empty
- How to Pass Spatial Reasoning Questions – Top Tips in 2024
- How to Improve Your Spatial Reasoning Ability
- Frequently Asked Questions
- Summary
What Are Spatial Ability Tests?
Spatial ability tests require you to use your cognitive ability to manipulate a 2 or 3 dimensional object to solve a question
Spatial aptitude tests often involve the visual assembly and the disassembly of objects that:
- Have been rotated
- Are viewed from different angles
- Have different markings on their surfaces
These tests bear a superficial resemblance to abstract reasoning tests, as both types of test usually contain a series of pictorial figures, rather than words or numbers.
Spatial ability however, does not involve analysis and reasoning. It is purely a test of mental manipulation.
Why Do Employers Use Spatial Reasoning Tests?
Employers use spatial ability questions when a job involves drawings, plans or the manipulation of shapes.
These are usually technical and design jobs; for example, architecture, engineering, surveying and design.
It is also important in some branches of science and technology where the ability to envisage the interactions of three-dimensional components is essential.
If you are applying for a job in the military, police or emergency services, then you may be asked spatial ability questions to do with maps or street plans.
You will need to show that you understand directions as they appear on a map and that you can use the map to plan, follow or describe routes.
People who score poorly on this test may have a tough time making it in these fields:
-
An architect, for instance, needs to be able to mentally rotate shapes and objects to effectively cover every aspect of the plans they are responsible for.
-
Engineers need to be able to envision all of the moving parts of their plans to be sure that their plans are well developed.
Why Do Employers Use Spatial Ability Tests?
More and more employers, hiring managers and university officials are adding this test type into their application and screening process before hiring or accepting a person into a program or job position.
Employers find spatial ability tests useful for the following reasons:
- They will identify candidates with the cognitive ability to perform the tasks of the job.
- They identify a candidate’s mental and cognitive skills and their ability to solve complex problems and plans.
- They are useful in narrowing down the pool of applicants.
- They reduce the time involved in screening potential employees.
If a person performs poorly in a spatial ability test it may demonstrate that, while they are great in an interview, they may not be able to perform the duties of the job they are applying for.
Prepare for Any Job Assessment Test with JobTestPrep
What to Expect on a Spatial Ability Test
Spatial ability tests will present various types of questions designed to test your spatial reasoning ability.
As we discovered above, these tests are normally part of the recruitment process, either before interview to narrow down candidates, or at the end of the process, before a final hiring decision is made.
You will usually be asked to sit a spatial reasoning test on a computer, either at the employer’s premises, during an assessment center or at home, via a link that will be emailed to you.
The questions will be visual, a series of shapes or patterns, and the answers will be in multiple-choice format.
There will usually be a strict time limit applied to the test and you won’t always be expected to complete every question.
Remember though that accuracy is equally as important, so don’t rush.
The employer will have an idea of the score that they expect you to reach.
This will normally be calculated by the test provider using a norm group and past test scores.
Prepare for Any Job Assessment Test with JobTestPrep
Examples of Spatial Reasoning Questions: 10 Types
1. Group Rotation
These are questions where a group of five or six two-dimensional shapes or elements are presented and you need to determine which groups are rotations of each other.
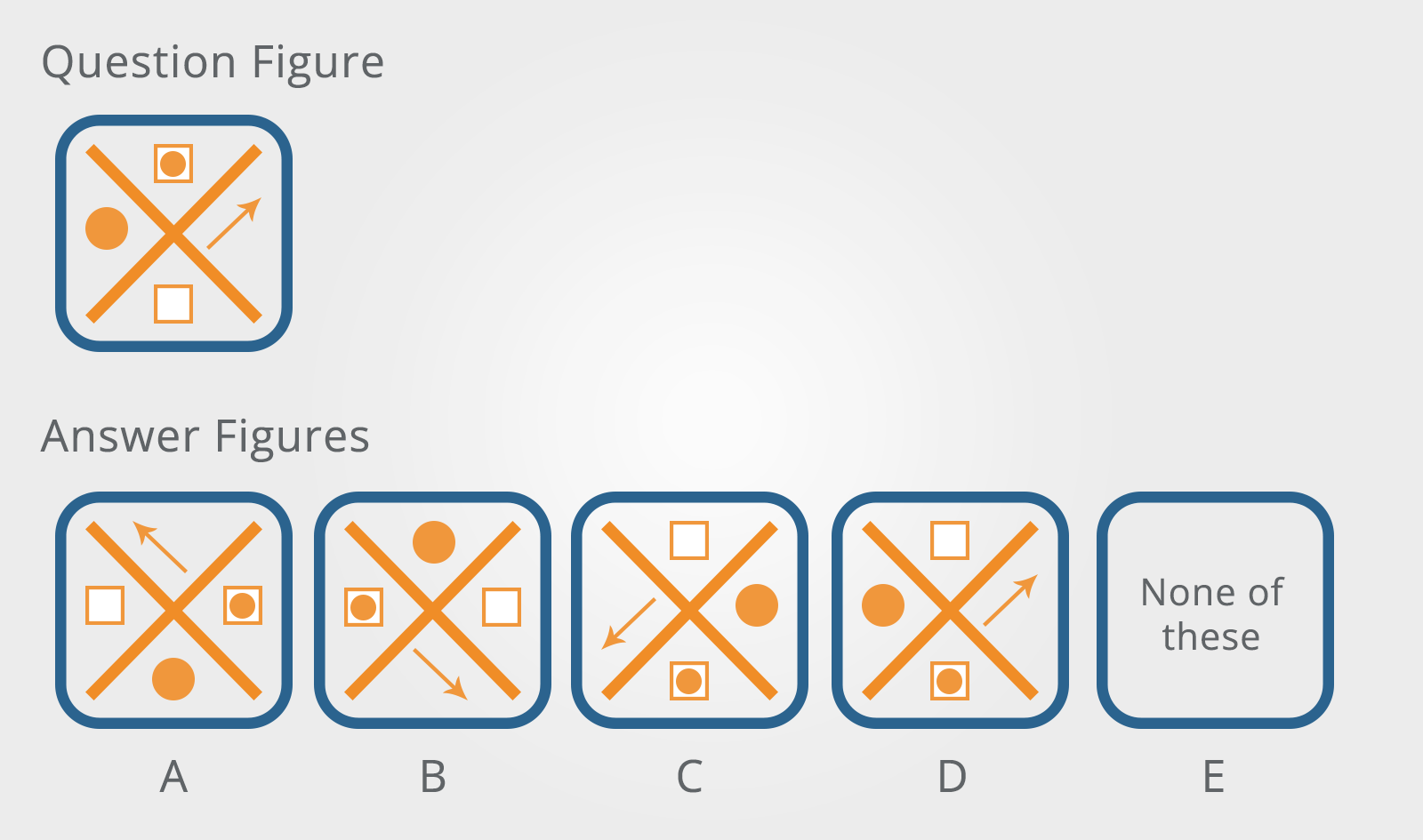
Which of the Answer Figures is a rotation of the Question Figure?
You need to be careful that you don’t identify reflections.
The best strategy is to choose the most asymmetrical shape in the group – in this case, the arrow.
Then determine the shapes clockwise, anticlockwise and opposite.
Thinking in these terms is more logical than using directions such as ‘right’, ‘left’, ‘above’ or ‘below’ as they are constant even when the figures are rotated.
In the example above, the white square is clockwise from the arrow. This means that A, B and D cannot be rotations of the Question Figure.
This leaves only C as a possibility which can quickly be checked element by element.
Remember that no logical manipulation of the figures is necessary, you are only interested in identifying which of the Answer Figures is identical to the Question Figure.
These spatial rotation questions are very common and are used in the tests supplied by many of the major test providers.
Because rotation only requires manipulation in two-dimensions, these questions are much easier than the three-dimensional cube questions.
2. Shape Matching
In this type of question, you will be presented with a number of objects, only two of which are identical.
These are speed questions and you will need to work quickly and attempt to answer as many as possible in the given time.
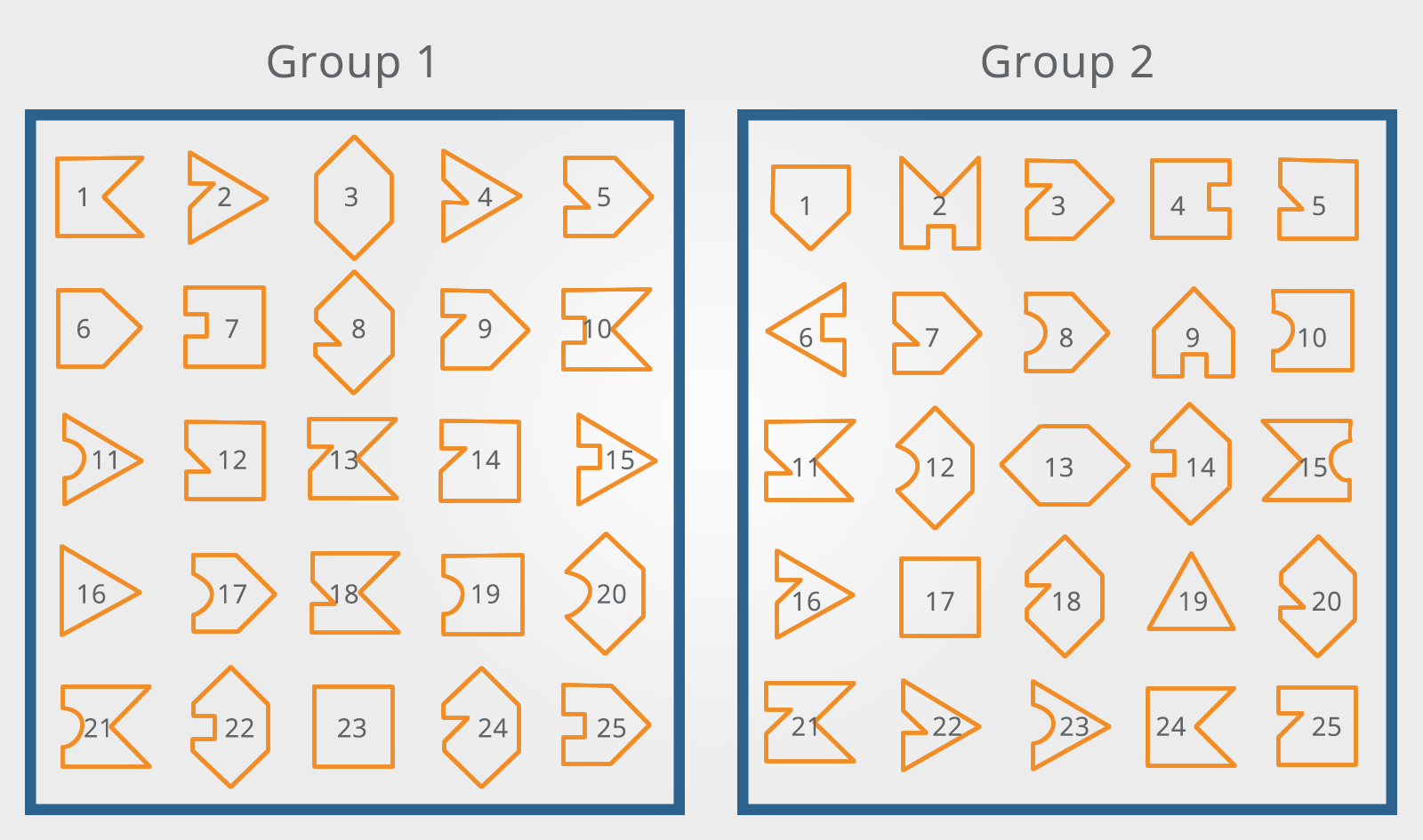
Which shape in Group 2 corresponds to the shape in Group 1?
In this example, you are asked to look at two groups of simple, flat objects and find pairs that are exactly the same size and shape.
Each group has about 25 small drawings of these two-dimensional objects.
The objects in the first group are labeled with numbers and are in numerical order.
The objects in the second group are labeled with letters and are in random order.
Each drawing in the first group is exactly the same as a drawing in the second group.
The objects in the second group have been moved and some have been rotated.
These questions use a large number of shapes that are presented close together.
Some people find this very distracting and find it easier to work through the shapes in the second group systematically.
In some questions of this type, there may not be a one-to-one match and some of the shapes in the first group may not appear in the second.
The way that the question is worded will make this clear.
If this is the case, then you should be especially careful to look out for reflections in the second group.
These are often put in by the test designers to trap the unsuspecting.
3. Visual Comparison
You will be presented with a number of objects, only two of which are identical.
Once again, these are speed questions and you will need to work quickly and attempt to answer as many as possible in the given time.

Which two pictures are identical?
If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
Prepare for Any Job Assessment Test with JobTestPrep
The best strategy for this type of question is to begin with the shape on the left and work through the shapes to the right of it systematically looking for an exact match.
If there isn’t one then move on to the second shape and repeat the process.
It can be quite difficult to discipline yourself to adopt this systematic approach to these types of question, as you may think that it is quicker just to look at all of the shapes until the answer jumps out at you.
The problem with this is that if the answer doesn’t jump out fairly quickly then panic sets in and you usually resort to the systematic approach anyway.
When you are confronted with a large number of similar types of question on a single page, the questions other than the one you are trying to answer can be distracting.
You may find that it helps to cover them and concentrate only on the two shapes that you are comparing.
Prepare for Any Job Assessment Test with JobTestPrep
4. Combining Shapes
These questions show you a series of two-dimensional shapes.
One of the shapes has been cut up into pieces.
The question presents you with the pieces and you are asked to work out which of the shapes has been cut up.
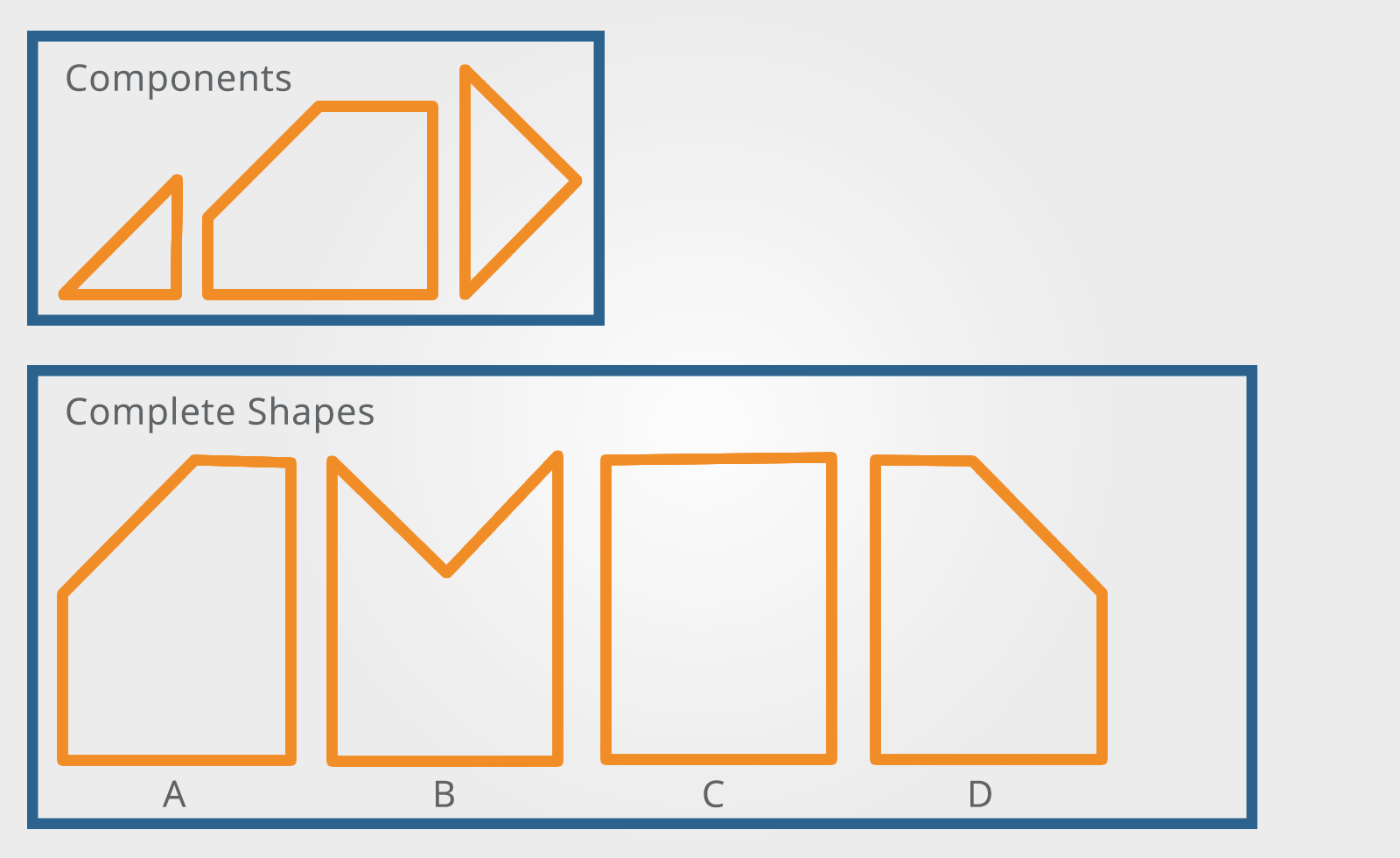
Which of the complete shapes can be made from the components shown?
The best strategy for answering these questions is to look at the complete shapes to see if there are any distinct features that would make it impossible to construct such a shape from the components.
In the example above, this is not very obvious but sometimes there are one or two shapes that can be immediately discounted based on size alone.
One thing to remember is that if the complete shapes don’t have any bits sticking out (they usually don’t) then the components must fit together so that sides of the same length are together.
This reduces the number of combinations considerably.
5. Cubes
These questions show you several (usually three) views of a three-dimensional cube with unique symbols or markings on each face.
Let’s look at an example question.

Three views of the same cube are shown above. Which symbol is opposite the X?
Some people seem to have a natural talent for imagining objects in three-dimensions and find these questions straightforward.
However, if you’re not one of them and you find thinking in three dimensions difficult, there are other ways to get the answer.
In the question above, for example, you can simply use a process of elimination.
If you can see a symbol on the same illustration as the ‘X’ then it cannot be opposite.
The second and third cubes eliminate A, B and C.
This leaves only D and ‘other’ as possibilities.
D has edges shared with A and B which would be consistent with the third cube illustrated.
Therefore, D is correct.
Although it is not usually specified in the instructions, it is almost always true that in these questions each symbol is used only once.
This means that even in cases where elimination is not possible, it is sometimes quite easy to see the solution without mentally manipulating the cube too much.
In the example above, you can simply compare the first and third illustrations.
The third illustration shows a 90-degree clockwise rotation (looking at the cube from above) of the first illustration.
Therefore D must be opposite the ‘X’.
6. Cubes in Two and Three-Dimensions
These questions show a flat (two-dimensional) pattern which can be folded to make a cube and a number of three-dimensional cubes (usually four).
The pattern and the cubes have symbols or markings on each face.
You need to look at the pattern and decide which of the cubes, if any, could be made from it.
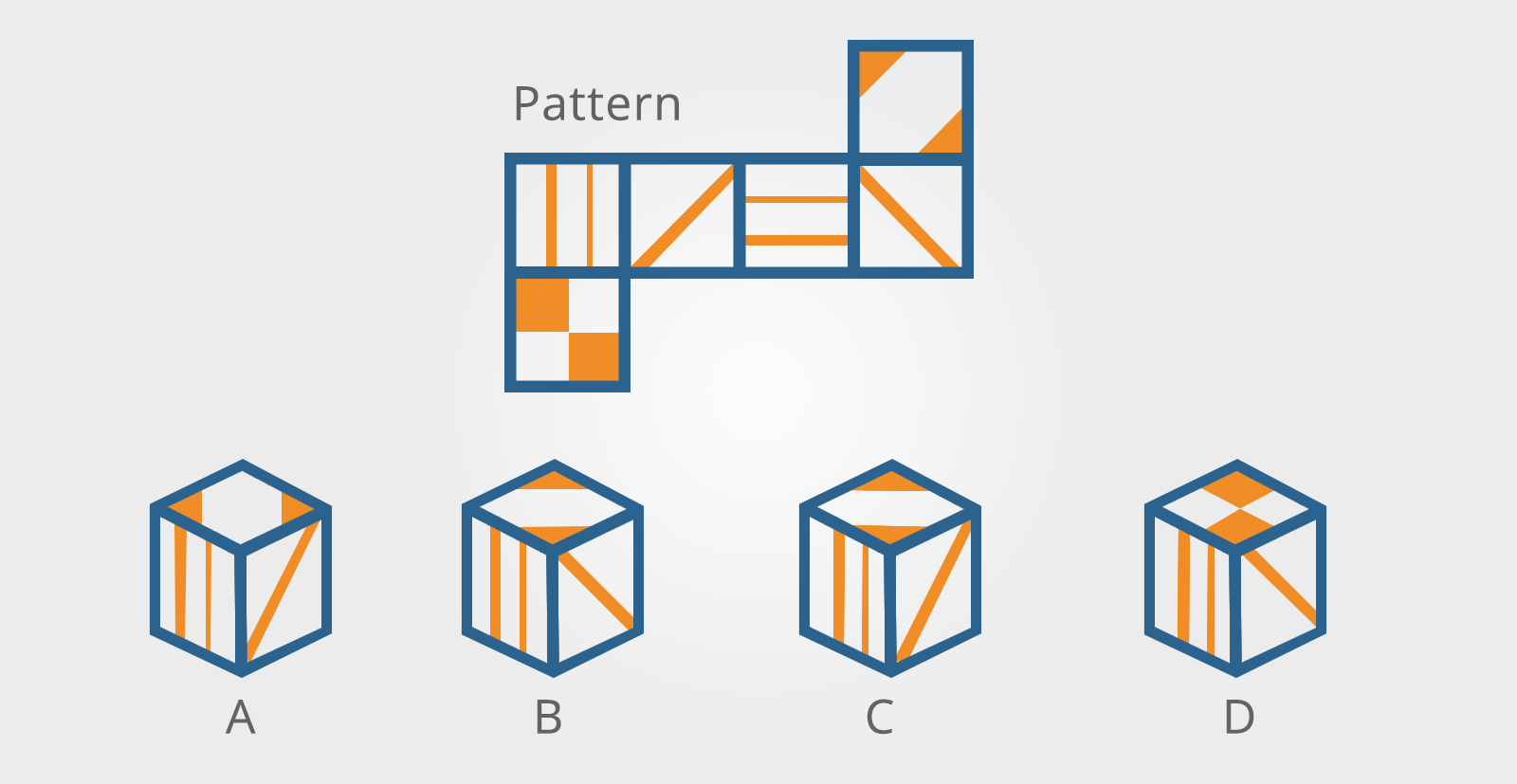
Which of the cubes shown could be made from the pattern?
The key to these questions is to remember that only three faces of the cube can be shown in the illustration, this means that you need only to consider the relationship between the three visible elements on each cube and see if the same relationship exists in the pattern.
The best strategy for this type of question is to call one face of the cube the ‘front’ and then to name the other faces of the cube in relation to it.
For example:
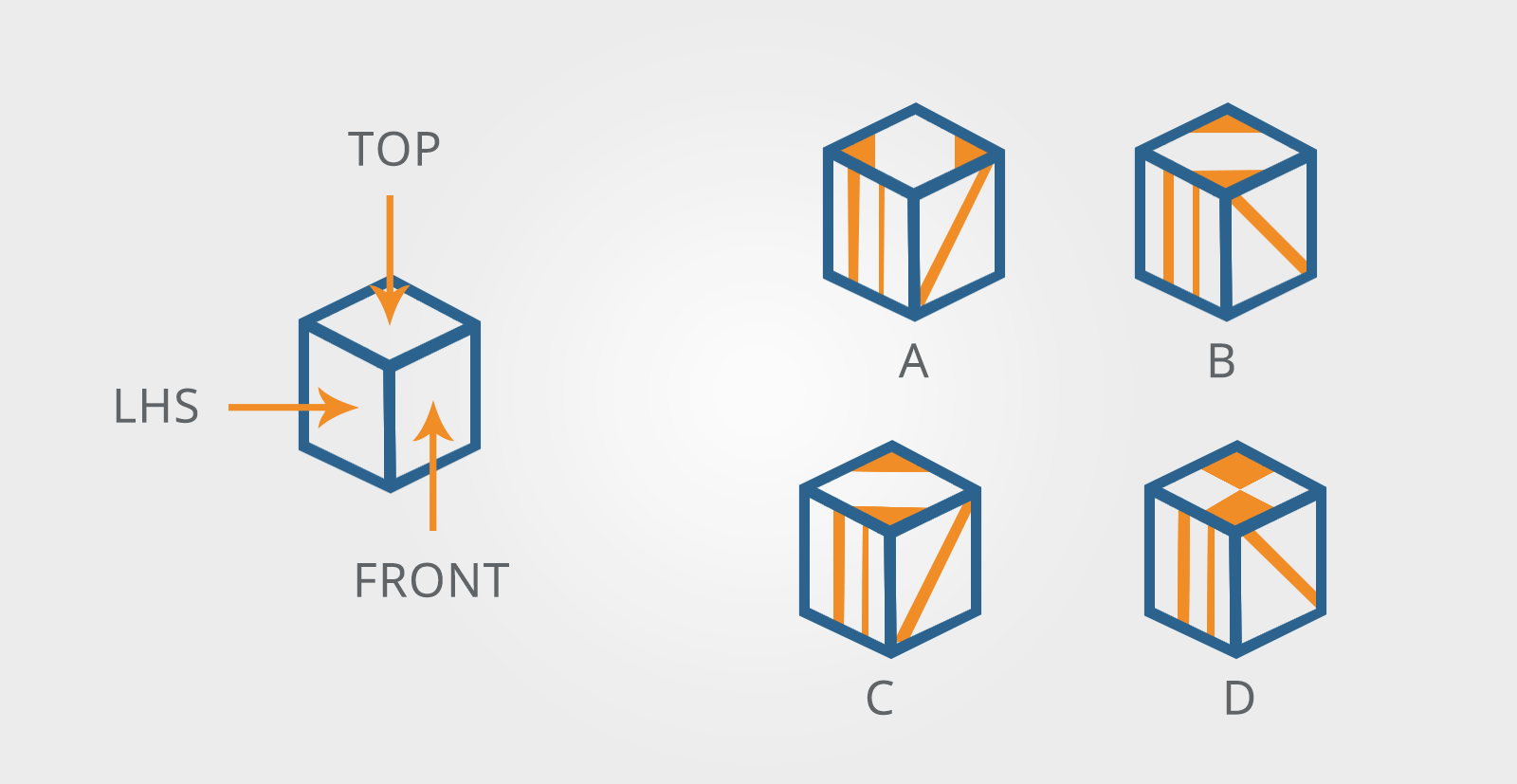
This is obviously an arbitrary decision as you could look at a cube from any side.
However, thinking of the problem this way makes it much easier to see the relationship between the faces of the cube.
You can then look at the front of the cube, find that face on the pattern, use the pattern to identify the ‘top’ and eliminate any options that do not match.
Use the pattern to identify the other face that touches the ‘front’ (in this example LHS) and eliminate any options that do not match.
Another type of question poses the problem the other way around.
Here you have a single three-dimensional cube and a number of two-dimensional patterns, only one of which when folded, will make the cube.
7. Solid Shapes
These questions are similar to the cube questions above but, rather than cubes, they use other solid shapes which may be irregular.
In some respects, these questions are easier than the cube questions as there are more relationships to work with.
In other words, each face of the solid shape has a shape of its own rather than just being square.
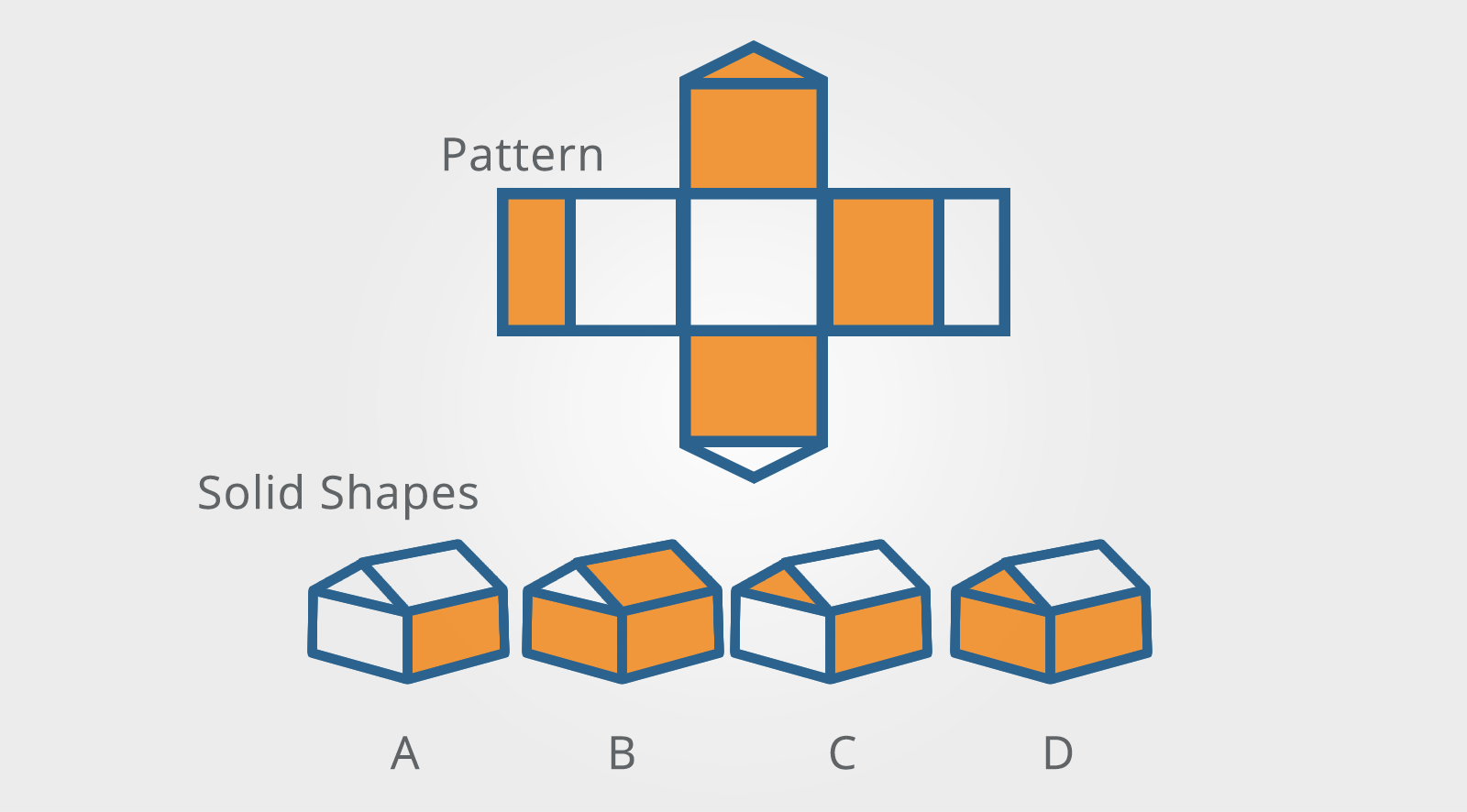
Which of the solid shapes shown could be made from the pattern?
Once again, you can reduce these problems to the relationship between the visible elements on the three-dimensional picture.
This makes things easier because even though the solid shape may have more faces than a cube, it is unusual for more than four faces to be shown.
This means that you need to consider the relationship between the four visible faces, paying particular attention to shading or other patterns on them.
8. Maps and Plans
These questions often appear in tests for emergency services, military and law enforcement jobs where the ability to give or follow directions based on a map or street plan is essential.
You will usually see an arrow showing which way is north. Sometimes, all four directions will be given (North, South, East and West), sometimes just North.
By convention, this is towards the top of the page.
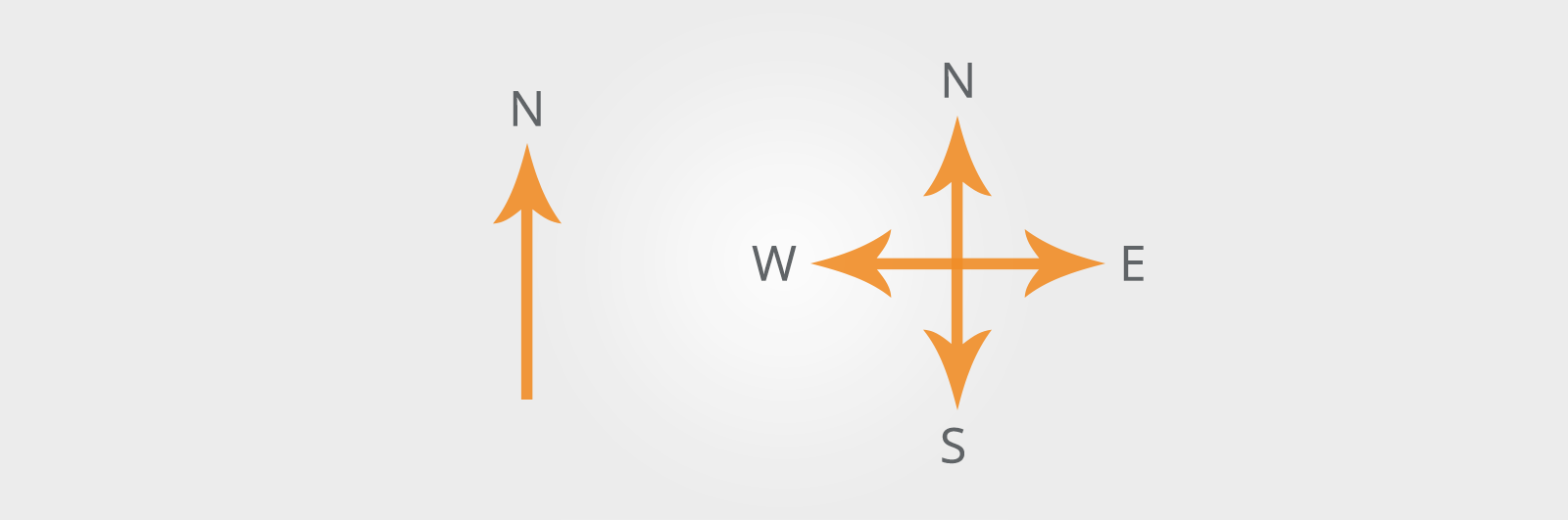
If only North is given, you can work out the others if you remember the saying ‘Never Eat Sour Wheat’ as this gives you all of the compass points reading clockwise from North.
You may also need to know the intermediate compass points as shown below:
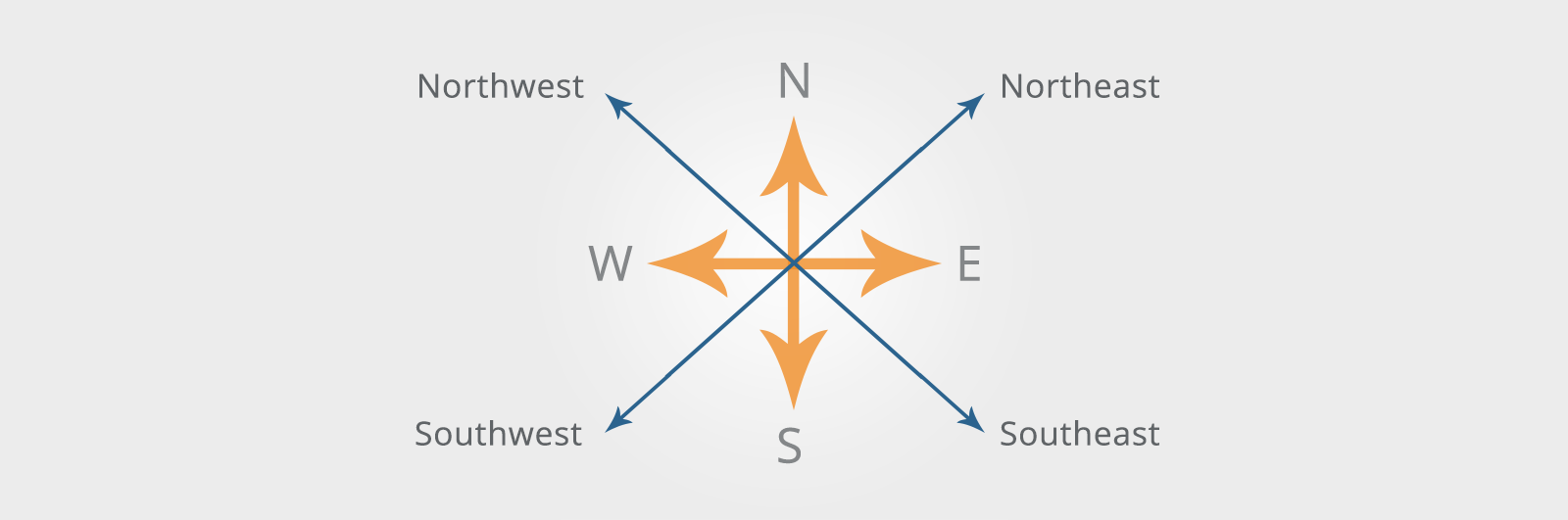
As well as knowing the points of the compass, you may also need to pay attention to traffic regulations if the question shows a city or town plan.
It is very common for these to show one-way streets which you can only drive down in the direction of the arrow.
You can, of course, walk in either direction and the question should make it clear whether you are walking or driving.
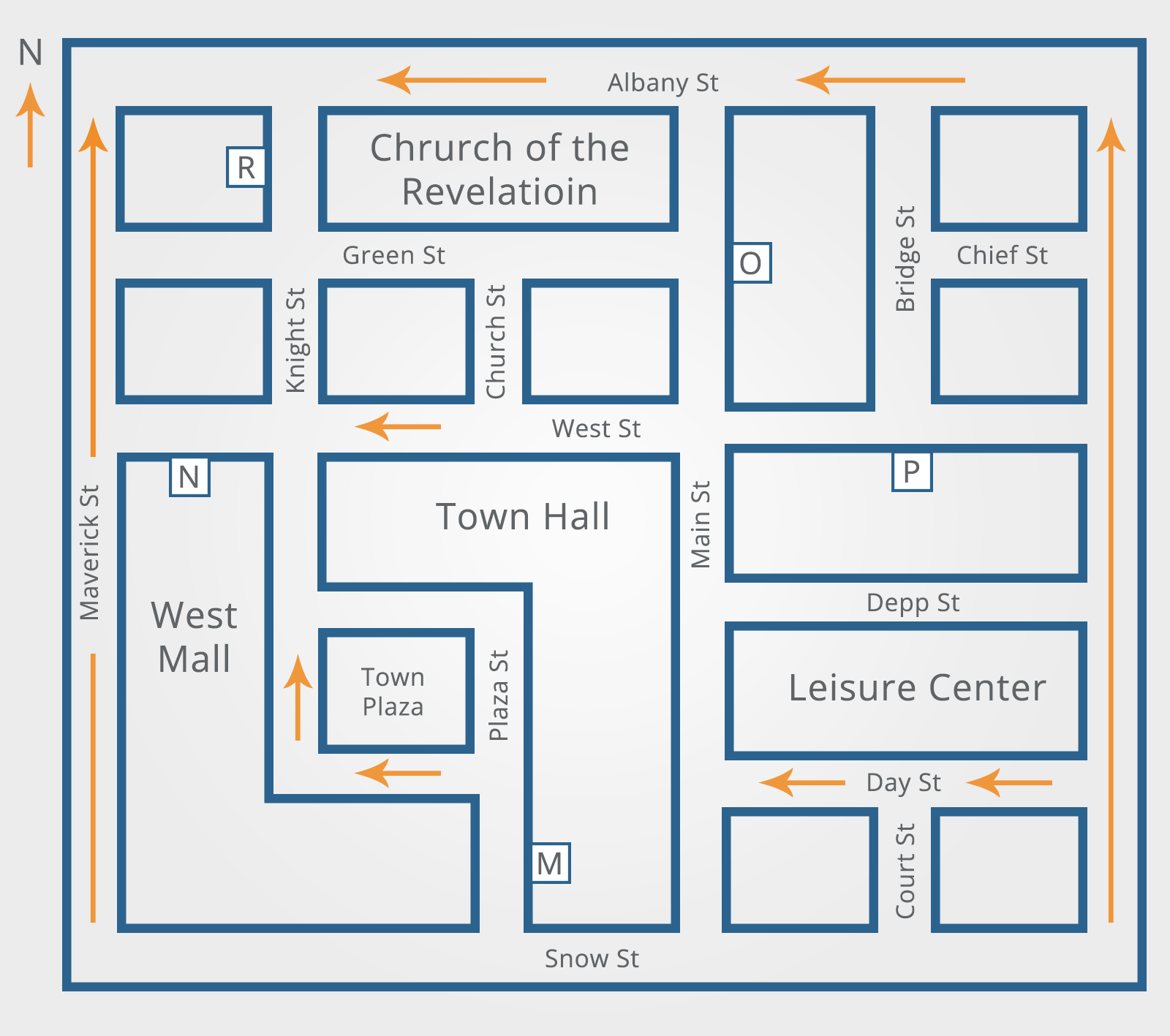
Officer Wilkinson is in Depp St and can see the Town Hall to her right. What direction is she facing?
A) North
B) South
C) East
D) West
She turns and walks to the junction with Main St. She turns left and proceeds two blocks before turning right, then takes the next right and walks half a block. Which location is nearest to her current position?
A) M
B) N
C) R
D) P
Officer Garcia starts from location ‘N’ and proceeds as follows: right onto West St – heading East, fourth left – heading North, first right – heading East, first right – heading South, third right – heading West. He proceeds West for one block. Where is location ‘P’ in relation to his current position?
A) North
B) South East
C) North East
D) North West
9. Block Counting
These questions consist of shapes formed from a group of three-dimensional blocks.
You will be asked to identify how many blocks have been used to make up the shape.
You will need to take into account the blocks that are hidden.
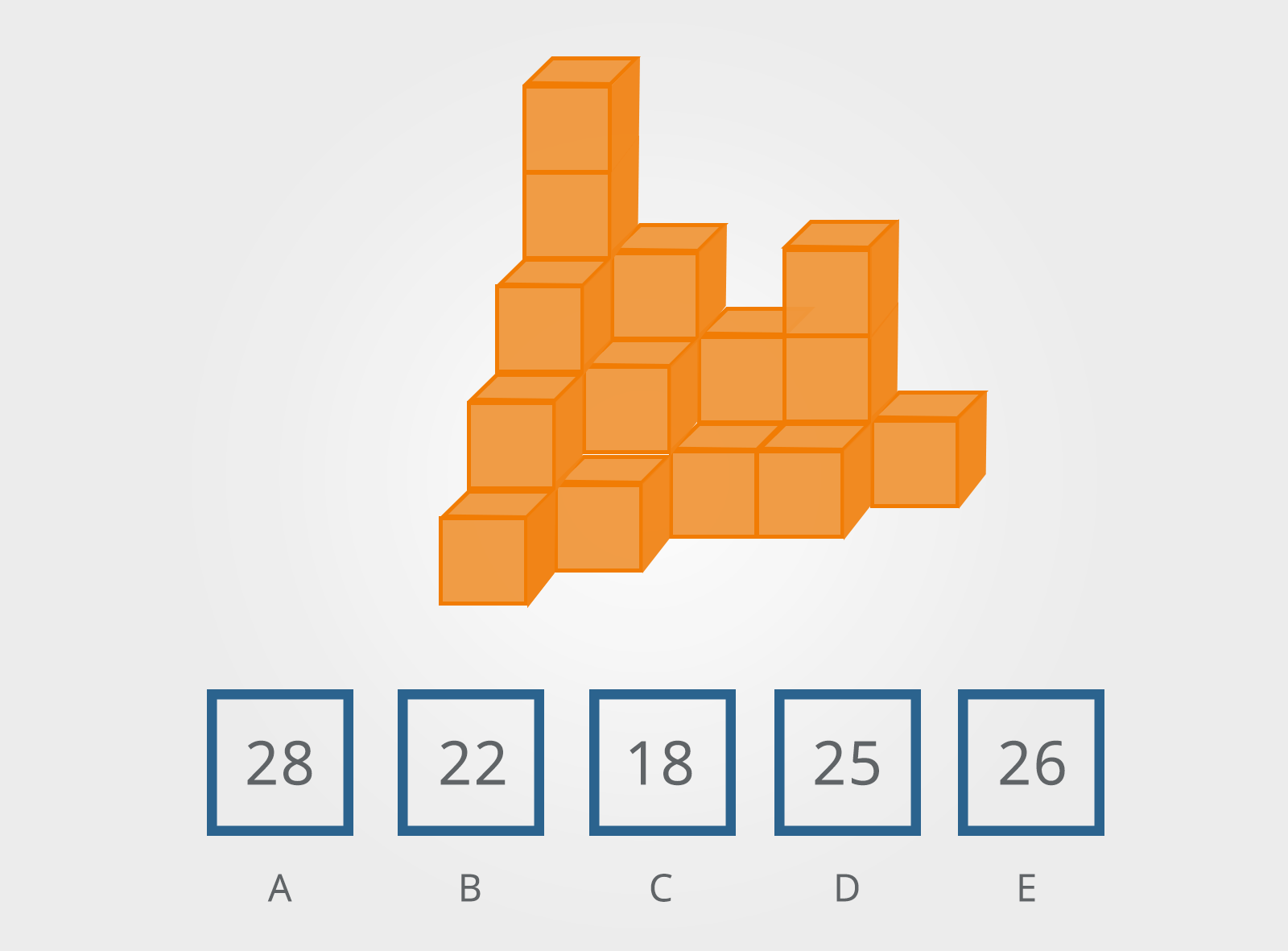
How many blocks make up the shape above?
10. Reflections
These questions will require you to identify the mirror image of a given shape or pattern.
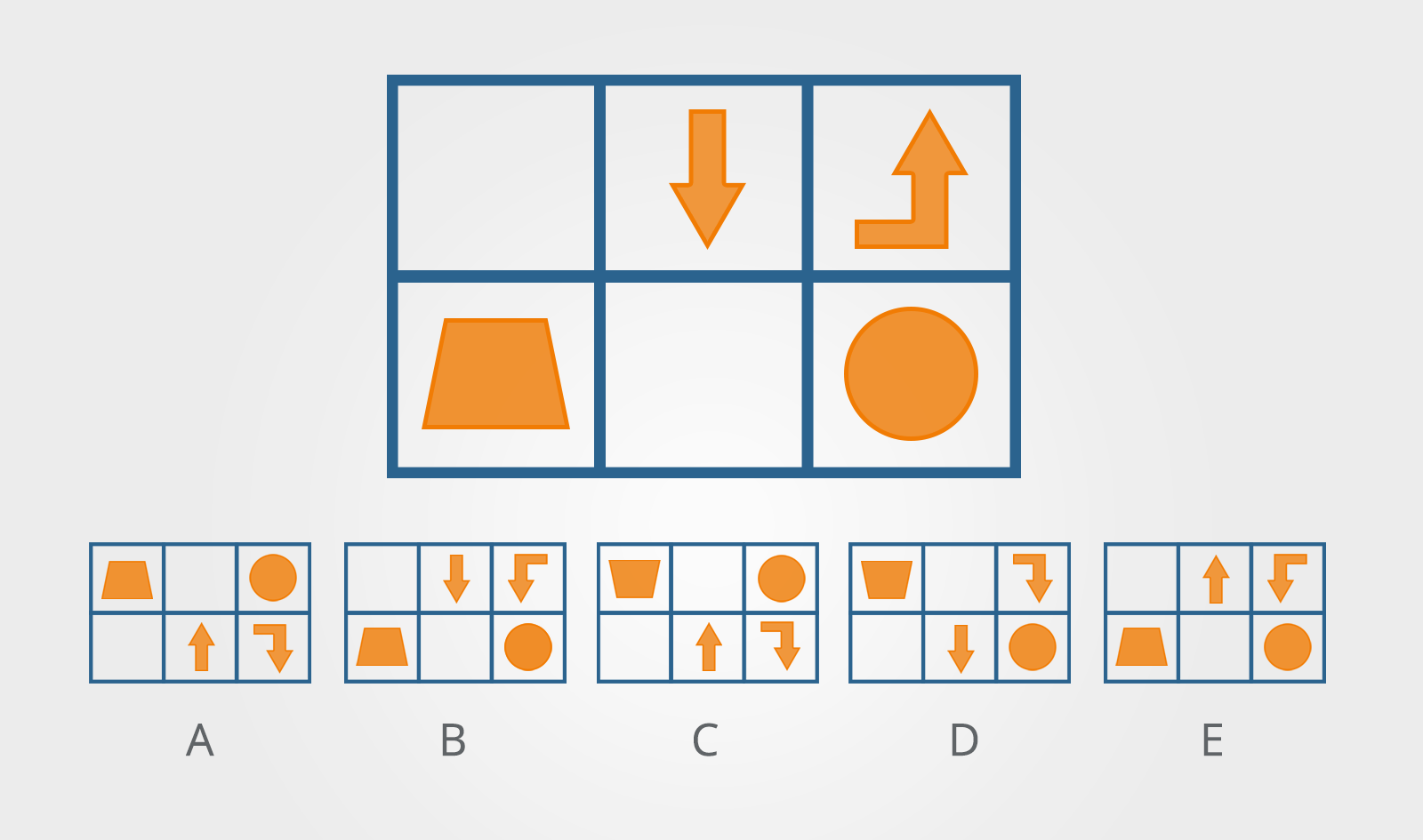
Which answer shows a mirror image of the image above?
Prepare for Any Job Assessment Test with JobTestPrep
How to Pass Spatial Reasoning Questions – Top Tips in 2024
Generally speaking, if spatial reasoning questions involve the manipulation of two-dimensional objects then they are probably fairly straightforward, but you will be challenged to answer them all in the time you are given.
If the questions involve the manipulation of three-dimensional objects then many people find them extremely difficult.
This is one skill that can be significantly improved with practice.
Remember, you are not looking for the logical relationship between figures – what you are trying to do is form mental images and visualize movement or change between them.
Here are some top tips for successfully completing spatial reasoning tests:
Step 1. Get Hold of Lots of Sample Questions
The only way to really improve your spatial reasoning is to practice all the different types of question until you are confident answering them.
When you get questions wrong, make sure you understand where you went wrong and how you can improve next time.
Step 2. Practice Working Quickly
Spatial reasoning tests are tricky because they usually have strict time constraints.
Most people would find the tasks relatively simple with endless time to complete them.
Ensure you practice using a stopwatch to ensure that you can complete the questions quickly and accurately.
Step 3. Do Not Guess
Some spatial tests deduct points for inaccurate work or wrong answers. Although you need to be fast, don’t forego accuracy. You will not always be expected to finish the test so make sure you are answering carefully.
How to Improve Your Spatial Reasoning Ability
Spatial ability involves visualizing and manipulating two and three-dimensional objects in your mind and understanding the relationships between objects as they are rotated or seen in mirror image.
About 5% of the adult population find it near-impossible to imagine two-dimensional shapes being moved through a third dimension.
This is thought to be because there is a genetic factor involved in spatial reasoning ability.
However, in general, spatial reasoning ability can be improved with practice.
Indeed, we use spatial reasoning every day in our normal daily interactions.
We visualize where things are in the house before we find them and organize the shopping in our car boots so that the eggs don’t get crushed.
If you find spatial reasoning tests hard, try to actively perform tasks like map reading or following two-dimensional plans to build three-dimensional things (such as flat-pack furniture).
Use mirrors to look at two and three-dimensional geometric shapes and patterns in reverse and practice drawing them out on paper.
Prepare for Any Job Assessment Test with JobTestPrep
Spatial awareness refers to the ability to perceive and understand the spatial relationships between objects in the environment.
It involves being aware of your body's position in space and how objects are positioned relative to each other. Spatial awareness allows individuals to navigate their surroundings, judge distances and manipulate objects accurately.
It plays a crucial role in activities such as driving, sports, architecture and many other everyday tasks.
The brain regions primarily responsible for spatial awareness are the parietal lobes, specifically the posterior parietal cortex. These areas integrate sensory information from various sources, including vision, touch and proprioception (sensing the position and movement of your body parts), to create a mental map of the surrounding space.
There is no universally defined "good" score for spatial reasoning tests because it can vary depending on the specific test and its scoring system. Scoring on spatial reasoning tests is typically percentile-based, where your score is compared to the scores of a group of people who have taken the same test.
A good score would be one that places you above the average or in a higher percentile, indicating a stronger spatial reasoning ability compared to the general population.
Spatial ability tests measure a range of skills related to spatial awareness and spatial reasoning, including:
Mental rotation: The ability to mentally manipulate and rotate objects in three-dimensional space.
Spatial visualization: The capacity to imagine and manipulate complex spatial patterns, such as folding or unfolding objects.
Spatial orientation: The ability to understand and work with directional concepts, like north, south, east, and west.
Spatial perception: The skill of recognizing and interpreting spatial relationships between objects and their positions.
Pattern recognition: Identifying regularities or patterns within complex spatial arrangements.
Visual-spatial memory: Remembering and reproducing spatial information after a brief exposure.
The duration of a spatial awareness test can vary widely depending on the specific test and its design. Some tests may be very brief, lasting only a few minutes, while others could take up to an hour or more. The duration often depends on the complexity of the tasks involved and the number of items or questions in the test. It's essential to follow the instructions provided for the specific test you are taking to manage your time effectively during the assessment.
Summary
Spatial reasoning tests can be particularly hard as they require you to use your mind to visualize shapes and patterns and how they might move or be manipulated.
This is a skill that can be significantly improved with practice.
Make sure you focus both on speed and accuracy and take plenty of practice tests before test day.





